и F6 можно вывести остальные,

Из аксиом Fl, F2 и F6 можно вывести остальные, а значит, они образуют полное подмножество для F1-F6. Аксиомы Fl, F2 и F6 являются также независимыми: ни одна из этих аксиом не может быть получена из двух других. Иногда эти три аксиомы называются аксиомами Армстронга.

Пусть  – множество F-зависимостей для отношения . Замыкание , обозначаемое , - это наименьшее содержащее  множество, такое, что при применении к нему аксиом Армстронга нельзя получить ни одной F-зависимости, не принадлежащей . Так как  должно быть конечно, то можно вычислить его, начиная с  путем применения Fl, F2 и F6 и добавления полученных F-зависимостей к  до тех пор, пока не перестанут получаться новые зависимости. Замыкание  зависит от схемы.

Из множества  можно вывести F-зависимость   , если  принадлежит . Так как аксиомы вывода порождают только функциональные зависимости, то  влечет за собой , если  выводится из .

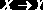
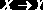
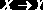
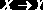
Пример 2.5. Пусть  – множество F-зависимостей на .

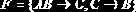
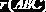
Тогда:







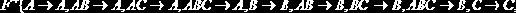
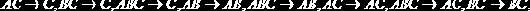
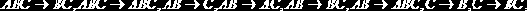
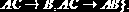
В свете   новых знаний об F-зависимостях, следует уточнить понятия ключа и суперключа.

Для данной схемы отношения  ключ – это подмножество, такое, что для любого допустимого отношения  не существует двух различных кортежей и  в , таких, что , и никакое собственное подмножество  не обладает этим свойством.

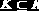
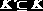
Для некоторых допустимых отношений со схемой подмножество  может быть ключом, но рассеются все допустимые отношения со схемой .

Суперключ – это любая совокупность атрибутов, содержащая ключ.

Нормализация – формальный метод анализа отношений на основе их первичного ключа (или потенциальных ключей) и существующих функциональных зависимостей [2, 7,10].

Цель нормализации – получение такого проекта базы данных, в котором каждый факт хранится в одном месте, т.е. исключена избыточность информации. Это делается не столько с целью экономии памяти, сколько для исключения возможной противоречивости хранимых данных из-за их избыточности.

Нормальная форма представляет собой ограничение на схему базы данных (отношения), которое избавляет базу данных от некоторых нежелательных свойств.


Содержание  Назад  Вперед

---

---