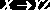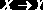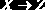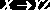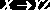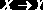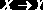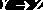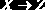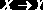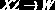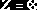Аксиомы вывода функциональных зависимостей
Для отношения
в любой момент существует некоторое семейство F-зависимостей, которым это отношение удовлетворяет. Здесь может возникнуть та же проблема, что и с ключами: одно состояние отношения может удовлетворять F-зависимости, а другое – нет.
Требуется выявить семейство F-зависимостей
, которому удовлетворяют все допустимые состояния
. Чтобы найти
, необходимы семантические знания об отношении
. Поэтому можно считать семейство F-зависимостей заданным в схеме отношения
. В этом случае любое отношение
должно удовлетворять всем F-зависимостям из
. Не всегда ясно, что является первичным: множество допустимых состояний отношения, которое определяет F-зависимости, или F-зависимости накладывают ограничения на схему отношения [10].
Множество функциональных зависимостей, применимых к отношению
, конечно, так как существует только конечное число подмножеств множества
. Таким образом, всегда можно найти все F-зависимости, которым удовлетворяет
. Однако этот подход требует большого количества шагов и, соответственно, много времени.
Если известны некоторые F-зависимости из
, то часто можно вывести остальные.
Множество F-зависимостей
влечет за собой зависимость
, если каждое отношение, удовлетворяющее всем зависимостям в F, удовлетворяет также зависимости
.
Аксиома вывода – это правило, устанавливающее, что если отношение удовлетворяет определенным F-зависимостям, то оно должно удовлетворять и некоторым другим F-зависимостям.
Сформулировано шесть аксиом вывода F-зависимостей [10]. В этих формулировках используется обозначение r для отношения на
и
,
,
и
– для подмножеств
.
Fl. Рефлексивность.
.
F2. Пополнение.
влечет за собой
.
F3. Аддитивность.
и
влечет за собой
.
F4. Проективность.
влечет за собой
.
F5. Транзитивность.
и
влечет за собой
.
F6. Псевдотранзитивность.
и
влечет за собой
.
Некоторые аксиомы вывода могут быть получены из других. Например, транзитивность F5 является частным случаем псевдотранзитивности F6 при
.
Приведенная система аксиом F1-F6 является полной. Это означает, что каждая F-зависимость, которая следует из множества Р, может быть выведена путем одно- или многократного применения к F этих аксиом.
Содержание раздела