Для уточнения оценок коэффициентов Сi,
Для уточнения оценок коэффициентов Сi, эксперту предлагается сравнивать четыре пары абстрактных объектов. Каждому объекту соответствует вектор х=(x1, x2, ..., хi, ..., x6), где xi=(0; 1): 1 –учитывается полезность i-го критерия, 0 – не учитывается; тогда:
1) (100000) хуже (011111);
2) (010000) лучше (001111);
3) (001000) хуже (000111);
4) (000100) лучше (000011).
Эксперт вынес систему решений. Соотношение x(1) лучше x(2) соответствует большей предпочтительности для эксперта объекта х(1) по сравнению с объектом х(2).
Непротиворечивость принятых решений должна подтверждаться выполнением системы неравенств:
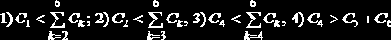
Проверка неравенств начинается с последнего (четвертого). Третье и четвертое неравенства выполняются, второе – нет; значит, необходимо скорректировать значения коэффициента С2. Примем значение С2=2. Однако одновременно необходимо изменить значение С1 таким образом, чтобы, во-первых, сохранился первоначальный порядок критериев, определенный экспертом, т. е. С1>С2, и, во-вторых, выполнялось первое неравенство. Принимаем, например, значение C1=2,5. В результате применения метода последовательных предпочтений получили непротиворечивый ряд оценок (табл. 2.5), которые в дальнейшем необходимо масштабировать.
Таблица 2.5
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
|
Ci |
2,5 |
2,0 |
0,7 |
0,6 |
0,3 |
1,0 |