Метод ранжировки
В соответствии с данным методом производится нумерация всех критериев полученного ряда, причем все неразличимые критерии, которые оказались на одном месте, нумеруются в произвольном порядке [3]. В результате данной процедуры каждый критерий получает свой номер. Ранг критерия определяется его номером, если на его месте в ряду отсутствуют какие-либо другие. Если на одном месте находится несколько неразличимых критериев, то ранг каждого из них равен среднему арифметическому их новых номеров.
Пример 2.2 ([3]). Пусть имеется следующий ряд упорядоченных критериев q1, q2, ..., q8 для j-го эксперта:
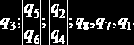
Ранги критериев, вычисленные в соответствии с вышеуказанной процедурой, сведены в табл. 2.2.
Таблица 2.2
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
rij |
8,0 |
4,5 |
1,0 |
4,5 |
2,5 |
2,5 |
7,0 |
6,0 |
Переход от рангов к коэффициентам Сij. производится на основе гипотезы о линейной зависимости между рангом и относительной ценностью критерия. Чем ниже ранг, тем более важным является соответствующий критерий. Определение коэффициентов Сij для произвольного rij(1 < rij £ п) производится в соответствии со следующей формулой:
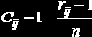
Для рассмотренного примера коэффициенты Сij сведены в табл. 2.3.
Таблица 2.3
|
i |
q1 |
q2 |
qз |
q4 |
q5 |
q6 |
q7 |
q8 |
|
Cij |
0,125 |
0,433 |
1,000 |
0,433 |
0,812 |
0,812 |
0,250 |
0,375 |
Следует отметить, что гипотеза о линейной зависимости между рангом и относительной ценностью критерия делает оценки Сij весьма грубыми, но определяет их сравнительно высокую достоверность.