в первом состоянии следует подвергнуть

Отношение в первом состоянии следует подвергнуть декомпозиции, ибо при заданном рейсе ДЕНЬ-НЕДЕЛИ не содержит информации об атрибуте ТИП-САМОЛЕТА, и наоборот.

Сформулируем это свойство по-другому. Если в отношении Назначение существуют кортежи  и , то должен быть кортеж . Формальное определение следующее [10].

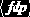
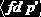
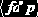
Пусть R – реляционная схема, X и Y - непересекающиеся подмножества R, и пусть Z=R–(XY). Отношение r(R) удовлетворяет многозначной зависимости (MV-зависимости) XУ, если для любых двух кортежей tl и t2 из r, для которых t1(X)=t2(X), в r существует кортеж t3, для которого выполняются соотношения t3(X)=t1(X), t3(Y)=t1(Y), t3(Z)=t2(Z).

Из симметрии определения относительно t1 и t2 следует, что в r

существует также t4 для которого

t4(X)=t1(X), t4(Y)=t1(Y), t4(Z)=t2(Z).

Пример 2.17. MV-зависимость РЕЙСДЕНЬ-НЕДЕЛИ выполняется для отношения Назначение в состоянии табл. 2.8, но не табл. 2.10. Состояние табл. 2.8 удовлетворяет также MV-зависимости РЕЙСТИП-САМОЛЕТА. Тот факт, что состояние отношения Назначение (табл.2.8) удовлетворяет двум MV-зависимостям, не является случайным [10].


Содержание  Назад  Вперед

---

---