Нормальная форма Бойса–Кодда (НФБК)

Схема отношения

 находится в нормальной форме Бойса-Кодда (НФБК) относительно множества F-зависимостей , если она находится в 1НФ и никакой атрибут в  не зависит транзитивно ни от одного ключа  [10].

Схема базы данных R находится в нормальной форте Бойса-Кодда (НФБК) относительно множества F-зависимостей

, если каждая схема отношения  находится в НФБК относительно . НФБК включает в себя ЗНФ [10].  

Схема отношения

 находится в нормальной форме Бойса-Кодда (НФБК) относительно множества F-зависимостей , если для каждого подмножества  из  и каждого атрибута  из  следует  при , т.е. если  нетривиально определяет произвольный атрибут из , то  есть сверхключ .

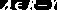
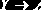
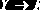
Для схемы отношения, не находящейся в НФБК, можно всегда провести декомпозицию в схему базы данных в НФБК [10].

С одной стороны, НФБК в некотором смысле является более сильной, чем 3НФ, а значит, более желательной. Но, с другой стороны, НФБК имеет свои проблемы [10]. Из предыдущего изложения следует, что при заданном множестве F-зависимостей над

 можно найти схему базы данных в ЗНФ, полностью характеризующую . Для НФБК это неверно. Множество F-зависимостей может не иметь полной НФБК схемы базы данных, кроме того, проверка свойства НФБК для заданной схемы базы данных является NP-полной задачей.

Пример 2.16. Пусть заданы схема

и . Атрибуты  являются ключом F, а В частично зависит от AD. При декомпозиции получаем

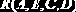
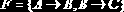
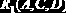
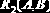
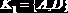
Несмотря на то чт R1, R2 формально находятся в ЗНФ, в Rl существует «скрытая» транзитивная зависимость С от AD.

Чтобы избежать проблем, возникающих при декомпозиции схем отношений, необходимо использовать другие методы получения третьей нормальной формы, например, метод синтеза ЗНФ [10].

2.4.3.8. Нормальная форма Бойса–Кодда (НФБК)

Схема отношения R находится в нормальной форме Бойса-Кодда

(НФБК) относительно множества F-зависимостей F, если она находится в 1НФ и никакой атрибут в Л не зависит транзитивно ни от одного ключа R [10].

Схема базы данных R находится в нормальной форме Бойса-Кодда

Содержание  Назад  Вперед

---

---