Оценка результатов экспертного анализа
При использовании всех рассмотренных выше методов возникает естественный вопрос: насколько можно доверять результатам оценки коэффициентов Сij, полученным из субъективных мнений экспертов? Достоверность результатов экспертного анализа чаще всего характеризуется степенью согласованности данных ими оценок. Для количественной оценки степени согласованности часто используется коэффициент конкордации [3]:
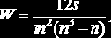
где
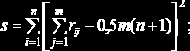
гij – место, которое заняло i-е свойство в ранжировке j-м экспертом.
Коэффициент W позволяет оценить, насколько согласованы между собой ряды предпочтительности, построенные каждым экспертом. Его значение находится в пределах 0£W£1, причем W=0 означает полную противоположность, а W=1 - полное совпадение ранжировок. Практически достоверность считается хорошей, если W=0,7¸0,8.
На основе рассмотренных методов могут быть определены значения коэффициентов Сij (j=1, 2, ..., m; i=1, 2, ..., п), по которым будут вычислены коэффициенты b., линейной формы интегрального критерия. При использовании такого подхода к формированию интегрального критерия в дальнейшем считается, что единица измерения каждого свойства системы, отраженного в соответствующем частном критерии, выбрана по принципу «чем больше, тем лучше». Отсюда следует, что качество решения по выбору альтернативы тем лучше, чем больше значение показателя эффективности.
Так как критерии qi могут иметь различную размерность, то при использовании их в качестве аргументов функции Е необходимо провести нормирование, т. е. привести их к общей размерности, и в частности к безразмерному виду.
Для придания равномерности влияния каждого из критериев на значение интегрального критерия необходимо выровнять диапазоны изменения значений критериев путем масштабирования и сведения их к диапазону [0; 1].
Проведение преобразований типов нормирования и масштабирования требует, чтобы для каждого из критериев были определены понятия «негодного» и «идеального» объектов, а это означает, что должны быть заданы допустимые области изменений значений критериев qi, qiн<qi<qiв. В этом случае самым простым масштабирующим и нормирующим преобразованием является линейное преобразование следующего вида: