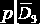Имеется несколько вариантов операции соединения:

Имеется несколько вариантов операции соединения:

а) тета- и эквисоединение. При этой операции A и B являются совместимыми атрибутами соединения, а степень результирующего отношения равна сумме степеней отношений-операндов. Такое соединение называется ?-соединением (тета-соединением). В случае сравнения на равенство соединение называется экви-соединение;

б) естественное соединение. В этом случае атрибуты соединения имеют общие (одинаковые) домены, и после соединения один из атрибутов отбрасывается. Степень результирующего отношения на единицу меньше суммы степеней отношений-операндов;

в) композиция. Это соединение отличается от естественного тем, что из результирующего отношения удаляются оба атрибута соединения. Поэтому степень результирующего отношения на две единицы меньше суммы степеней отношений-операндов.

Примеры

Тета-соединение R[Q>A]S

При выполнении соединения необходимо для каждого кортежа из R взять значение атрибута Q и сравнить его со значением атрибута A из каждого кортежа S. В результате получим



Следует отметить, что кортеж <w 50 1 b> отношения R не вошел в результирующее отношение.

Естественное соединение P[D3 =D4]Q



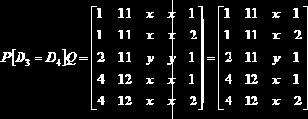
Деление

Алгебра	Исчисление
R[A÷B]S	{r[ ] | r ?R  ?s ?S[B] gR(r[ ])}

Атрибуты A и

B являются совместимыми и/или общими атрибутами деления. Для упрощения объяснения можно считать R бинарным отношением, состоящим из A и дополнения A, которое обозначается  и содержит атрибуты, отличные от A. Для каждого раздела из R[], т.е. для каждого уникального кортежа r[], необходимо выполнить следующее:

•         выбрать допустимые строки кортежей r[]

из R[], обозначив полученное множество кортежей через T=gR(r[]). Множество T называется также множеством-образом;

•         в результирующее отношение входят кортежи r, для которых выполняется S[B]HgR(r[]).

Примеры

Р[D3>÷D4]=Ø (пустое множество), так как





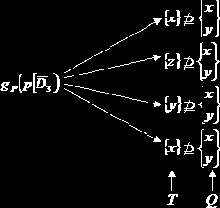
Следовательно, подходящие  отсутствуют.


Содержание раздела

---

---