в качестве формулы выступает конструкция

Например, выражение {t| R1(t) ?R2(t)}, где в качестве формулы выступает конструкция R1(t) ?R2(t), означает, что необходимо получить множество всех кортежей t, причем таких кортежей, которые принадлежат отношениям R1 или R2. Формула (R1(t) ?R2(t))) имеет смысл только тогда, когда отношения R1 и R2 имеют одинаковую арность, поскольку переменная-кортеж t задана как переменная фиксированной длины. Выражение { t| R1(t) ?R2(t)} эквивалентно операции объединения (R1

R2

реляционной алгебры.

Формулы в реляционном исчислении строятся из атомов и совокупности арифметических и логических операторов.

Атомы формул могут быть трех типов [17]:

1) R(t), где R – имя отношения. Этот атом означает, что t – это кортеж в отношении R;

2) s[i]?u[j], где s и u - переменные-кортежи; ? – арифметический оператор (<, >, =, ?, ?, ?); i, j – номера или имена необходимых компонентов (столбцов) в соответствующих кортежах; s[i] – i-тый компонент в кортеже-переменной s; u[j] - j-тый компонент в кортеже-переменной и. Например, атом (s[3] ? u[5]) означает, что третий компонент переменной s больше или равен пятому компоненту переменной u;

3) s[i]?a или a?s[i], где a – константа. Например, атом (s[4]=70), означает, что четвертая компонента переменной-кортежа s

равна 70.

При записи формул используется понятие свободных и связанных переменных-кортежей, что определяется характером использования в формуле кванторов;

– квантор всеобщности (общности), читается – все, всякий, каков бы ни был и т.п.;

– квантор существования, читается – некоторые, хотя бы один существует и т.п.

Вхождение переменной t в формулу ? связано, если в ? оно находится в подформуле, начинающейся квантором

или

, за которым непосредственно следует переменная t и о котором говорят, что он связывает переменную t. В остальных случаях вхождения переменной t в формулу ? свободны. Например, в формуле

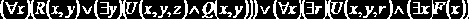
все вхождения переменной x связаны, первое и последнее вхождения y свободны, остальные вхождения переменной y связаны, все вхождения переменной z свободны, единственное вхождение переменной r связано.

Содержание Назад Вперед