существует некоторый кортеж s, принадлежащий
Например, формула (

5. Формулы могут при необходимости заключаться в скобки. Используется следующий порядок старшинства:
§ арифметические операторы сравнения;
§ кванторы


§ ?, ?, ¬.
6. Ничто иное не является формулой.
В качестве примера можно записать выражение реляционного исчисления на переменных-кортежах, соответствующее операции проекции в реляционной алгебре:
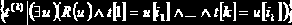
Введем ограничения на конечность реальных отношений в БД, чтобы исключить возможность формирования выражений типа {t|-R(t)}, не имеющих смысла. Это выражение обозначает все возможные, не принадлежащие R кортежи, арность которых согласуется с t.
С этой целью в реляционном исчислении рассматривают только безопасные выражения {t|?(t)}, для которых выполняется условие, что каждый компонент (элемент столбца) любого кортежа t, удовлетворяющего ?(t) является элементом некоторого множества элементов D(?). Множество D(?) определяется как функция фактических отношений, которые указываются в ?(t), и констант, присутствующих в формуле ?(t) и элементов кортежей тех отношений, которые указаны в ?(t). Так как все отношения в БД предполагаются конечными, то и множество D(?) – конечно:
D(?)={a1.?}







где a1.?, a2.?, ..., an.? – константы, встретившиеся в формуле ?(t); ?1(R1), …, ?k(Rn) – проекции кортежей фактических отношений R1, ..., Rn, встретившихся в формуле ?(t) (в данном случае – компоненты кортежей).
При таком определении множества D(?) справедливо следующее:
D(?1(t) ??2(t))= D(?1)

D(?1(t) ??2(t))= D(?1)

D(?1(t) ?¬?2(t))= D(?1)

Например, если задано выражение {t|c ?R(t)}, где R – бинарное отношение, то
D(?)={c}

